ESR te hoog of DC lekkage, wat gaat er dan mis ?

@Omicron: sorry, maar met 'alletwee' bedoelde ik jou niet.
Het is een beetje flauw om steeds met die amplitude aan te komen. Dat weten de meesten al wel; ik heb zelf de formule al neergezet.

Als bij dezelfde amplitude de golfvorm toch steilere flanken bevat, dan kan dat alleen door hogere frequentiecomponenten toe te laten in het spectrum.
Als dat niet waar was, zou de flanksteilheid gelijk blijven ook al pas je een laagdoorlaatfiltering toe.

De slew rate van de opamp beperkt ook de bandbreedte bij grote signalen. Zelfde verhaal: hij kan niet steil genoeg.

en zelfs dan klopt het nog voor geen meter.

je kan Dv/Dt of Di/Dt met niks maar dan ook niks relateren. noch met amplitude noch met frequentie.

pak een sinus van gelijk welke frequentie. laten we zeeggen 1Hz.
de positieve top van de sinus is 1 volt piek ( 2 volt piek to piek ).

de positieve alternantie is 180 graden of een halve seconde. het duurt dus 1/4 seconde om van 0 volt naar 1 volt te gaan

we gaan een aantal dv/dt bepalen
- bepaal dv/dt van 0 graden naar 45 graden ..
- bepaal dv/dt van 45 graden naar 90 graden...
- de dv/dt van 0 graden naar 90 graden is 4v/s ( we zijn 1 volt gestegen in 1/4 van de alternantie)
- de dv/dt over de ganse periode van de sinus is NUL
- de dv/dt van 135 graden naar 235 graden is dan weer 8 volt /s

conclusie : je kan noch amplitude noch frequentie gebruiken om dv/dt of di/dt te beschrijven ! dat heeft NIKS met elkaar te maken !

dv/dt is gedefinieerd op een edge en je moet opgeven van waar tot waar je meet. ik ga van zoveel volt naar zoveelt volt . hoe lang duurt dat ? zo lang. ok, dan is mijn dv/dt in die tijdspanne zoveel.

Alle andere informatie is op dat moment verloren. wat was de totale amplitude van het signaal? watr was de frequentie van het signaal ? .. lost.

[Bericht gewijzigd door free_electron op maandag 26 april 2010 23:40:47 (20%)]

Mea culpa als mijn opmerking als flauw wordt gezien. Maar je kan veel veronderstellen over wat een ander al dan niet weet. Feit is dat dV/dt en bandbreedte dikwijls door elkaar gehaald worden. Als je correct bent in je terminologie dan zal iedereen die iets probeert bij te leren daar alleen maar voordeel bij hebben.

Zijn er constraints op dV/dt of dI/dt dan zit je in het tijdsdomein te ontwerpen. Een fourier spectrum helpt je in dat geval geen stap verder bij het ontwerpen van je schakeling. Het enige wat je interesseert is de golfvorm in het tijdsdomein.

Zijn er constraints op de bandbreedte: dan zit je in het frequentie domein te ontwerpen. Dan interesseert de golfvorm je geen bal en kijk je enkel naar het spectrum.

Mij lijkt het dus wel degelijk belangrijk om duidelijk te zijn als je over het gedrag van een component praat. Wat is het nu dat belangrijk is: de dI/dt of de bandbreedte? In mijn boekje een groot verschil.

Op 26 april 2010 23:37:13 schreef Omicron:
Feit is dat dV/dt en bandbreedte dikwijls door elkaar gehaald worden.

juist. ik kan perfect een 1volt blokgolf van 1MHz door een unity-gain opamp met een bandbreedte van 1MHz sturen. ( we gaan er even van uit dat unity gain in dit geval betekent dat er nog geen verzwwakking optreedt, in het echt is dat al het -3db punt maar we gberuiken voor het hoogfdrekenen effe het 0db punt)

De amplitude blijft identiek. de frequentie ook.
de DV/DT aan de uitgang van 0% naar 100% op de positive edge zal 4v/microseconde zijn. ( 1/4 van de periode om 1 volt te stijgen en de periode is 1 us)

wat is de dv/dt aan de ingang ? dat kon evengoed 5 teravolt per attoseconde geweest zijn (en daar zitten geweldige fourier elementen in, maar die komen er niet door aan de uitgang !). die opamp volgt op zijn eigen tempo en die superstrakke blokgolf komt daar gewoon als sinus uit. dv/dt is serieus verandert tussne in en uitgang. en toch is zowel amplitude als frequentie identiek gebleven. als die uitgang gewoon die slew rate niet aan kan helpt daar geen lievemoederen aan.

vandaar , nog eens : dv/dt en di/dt hebben niks met frequentie of amplitude te maken. je verliest te veel informatie op het moment dat je dv/dt uitrekent.

frequentie is 1/ periode van een signaal. (een periode is gedefineerd als de tijdspanne waarna het signaal herbegint.)

dv / dt ? hangt er vanaf. soms is dat 0 tot 100% , soms 10 /tot 90. soms is het gedefineerd als een bepaalde tijdsduur ( van tijd x naar y) binnin een periode van een signaal.

om de correcte opamp te kunnen definieren zou ik er ene nodig hebben met een oneindig ebandbreedte. pas dan kan ik de ingang volgen.
praktisch is dat larie en apekool. dat bestaat gewoon niet. daarom zeggen we : ik heb een opamp nodig die 10v/us doet. je kijkt wat er in gaat en met die slew rate is dat signaal aan de uitgang bruikbaar.
als die amplitude aan de uitgang 1 volt is : x bandbreedte nodig.
als de amplitude 10 volt is : das een compleet andere bandbreedte !

[Bericht gewijzigd door free_electron op maandag 26 april 2010 23:57:38 (13%)]

Natuurlijk verandert die steilheid in een eenvoudige sinus.
Vandaar dat ik ook zei: dI/dt = A ω cos(ω t)
De term A ω is de maximale steilheid, maar daarachter komt de tijdsafhankelijke term.
Dat was alleen om te laten zien in hoeverre Omicron's amplitude ermee van doen heeft. In niet-sinusvormige signalen zul je verder moeten kijken.

Als je die arme opamp uit Free's voorbeeld vervangt door één die de blok beter benadert, dat wil zeggen, met een steilere flank, dan zal NATUURLIJK de herhalingsfrequentie van die blok gelijk gebleven zijn.
Maar in het spectrum van de golfvorm aan de uitgang zullen de hogere harmonischen nu sterker geworden zijn.

Op 26 april 2010 22:57:15 schreef Frederick E. Terman:
Als bij dezelfde amplitude de golfvorm toch steilere flanken bevat, dan kan dat alleen door hogere frequentiecomponenten toe te laten in het spectrum.

Ben je daar wel helemaal zeker van?

Ga even mee in het volgende gedachten experiment: je begint met een driehoek signaal. We weten dat dat signaal een spectrum heeft dat doorloopt tot in het oneindige. Laat er ons wat getallen op kleven: we kiezen een frequentie van 1Hz en een amplitude van 1Volt. We hebben dus een dV/dt van 1V op 0.25 sec of 4V/sec.

Stuur dat nu door een laagdoorlaatfilter. We filteren alle frequenties weg behalve de grondtoon van 1Hz. Volgens mijn polytechnisch zakboekje geeft dat een sinus met een amplitude van 8/(pi*pi), m.a.w. een amplitude die iets kleiner is dan 1 V. De maximale dV/dt van deze sinus is 2*pi*1*8/(pi*pi) = 5V/sec.

Verassing verassing...ik stuur mijn signaal door een laagdoorlaat filter en in het resultaat komt een HOGERE dV/dt voor!

Dat heb je vast nooit geprobeerd.

Daarom is het een gedachten experiment he

Maar als je een fout ziet in mijn redenering...

Ha, ha! Het is verdikkie nog waar ook. Dat heb je knap (en snel!) bedacht, moet ik zeggen.

(denkt snel na) Natuurlijk kan een hogere harmonische ook tegenwerken..

Op 26 april 2010 21:59:13 schreef Omicron:
[...]Maar enfin! Dat is gewoonweg niet waar! Er is geen enkel verband tussen het fourier spectrum en de dV/dt. Voor een puls klopt dat toevallig ja, maar in het algemeen is dat niet waar!

Het beste bewijs: neem een sinus van 1Hz. Drijf de amplitude op en de dV/dt gaat omhoog. Kijk naar het spectrum: nog steeds identiek hetzelfde.

Ik begeef me nu op glad ijs in deze strijd der titanen maar jullie praten langs elkaar heen denk ik. Als de steilheid toeneemt dan verandert het fourier spectrum. Het wordt meer blokgolf. Dat weet ik zelfs terwijl ik geen fourier kan berekenen. Als de amplitude toeneemt bij de zelfde frequentie dan veranderd de steilheid namelijk niet maar wel de "stijgtijd" (denk ik)

Maar nog steeds weet ik niet of mijn stelling klopt dat je de capaciteit bepaald op de genoemde graden (voor de duidelijkheid nogmaals, niet graden celcius)

Oja: ik bedoel het zoals je het op een vna scherm ziet. 360 graden is een heel rondje om de smith kaart heen. >0 tot <180 graden is inductief. De negatieve variant is capacitief. Bij 0 en 180 is er resonantie. Ik dacht zelf dat precies op -90 graden (dus de bodem van de smith kaart het meetpunt was maar ik ben al een paar keer dus waarden tussen de 45 en 60 graden tegen gekomen. Daar klopt de waarde ook aardig met wat lcr meters er van maken.

[Bericht gewijzigd door fred101 op dinsdag 27 april 2010 00:56:03 (19%)]

Gelukkig, ik kan alsnog slapen straks: inderdaad werkt, bij de nuldoorgangen, een hogere harmonische tegen qua steilheid. Hier zie je de grondfrequentie en de derde harmonische in de zaagtand (let op, hier is de sinus zelf al 1V):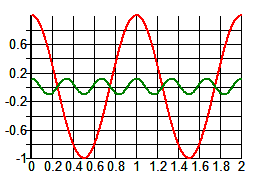

Toch is de driehoek natuurlijk 'gemiddeld steiler'; de sinus houdt zijn steilheid niet enige tijd vol, om zo maar te zeggen.

Maar dit is inderdaad een omdraaiing. Ik denk dat iedereen overigens wel weet wat er, ruwweg, van een bepaalde golfvorm te verwachten is wat het spectrum betreft. Maar dit was een leuke!

Fred, eerlijk gezegd weet ik niet wat je bedoelt met de graden. Ik had er nooit over gehoord tot je erover begon.

Ik zou me nog kunnen voorstellen (maar nu zit ik te raden) dat je een meetfrequentie uitzoekt, waarbij de reactantie van het zuivere capaciteitsaandeel (X_C) en de serieweerstand (hoofdzakelijk ESR) ongeveer even groot zijn. Je zou dat kunnen willen omdat je anders makkelijk een relatief grote meetfout zou maken in de kleinste van de twee.

Als dat zo is, dan is er een faseverschil van ongeveer 45 graden tussen spanning en stroom in die gecombineerde keten R_ESR + X_C. Bedoel je dat soms?

Iets dergelijks zou je ook kunnen zeggen van de C-meet-methode met een meetgenerator en een bekende serieweerstand, trouwens (waarbij je dan wel weer de ESR verwaarloost, natuurlijk ).

Interessante discussie, maar het ging in eerste instantie toch over de maximale piekstroom die je uit een condensator kan trekken? Dan is de di/dt toch totaal niet relevant, het gaat dan juist om de amplitude. Of eigenlijk de tijdsintegraal van het kwadraat ervan, want het probleem is dat die cap opwarmt doordat er een stroom door zijn ESR loopt, en daarin dus I²R aan vermogen dissipeert.

Bij een condensator is de stroom toevallig evenredig met dv/dt, maar dat is toch een wat vreemde waarde om aan te geven. Zeg dan gewoon stroom

Of heeft werkelijk de steilheid van de stroompiek nog een bepaald effect op een condensator (ESL daargelaten)?

De oorspronkelijke vraag, daar zeg je wat!

Op 22 april 2010 23:20:40 schreef fred101:
Ik dacht dat ik wist wat ESR was. De serie weerstand die een condensator vertoond. Maar nu begrijp ik dat hij waardoor wel stroom opneemt maar pas met een soort vertraging weer vrij geeft. Dat begrijp ik tenminste uit het scoop plaatje hier.

Dit is het plaatje:

Hier is geen vertraging te zien hoor! Die stap is een spanningsstap, geen tijdstap.
Wat je ziet is gewoon dat er bij opladen spanning over de ESR valt, en bij ontladen ook, maar dan uiteraard andersom (de stroom erdoor is dan omgekeerd).
Dus als je met, ik noem maar wat, 0,2A oplaadt en ook met 0,2A ontlaadt, en de ESR is 0,6 ohm, dan valt er bij opladen 0,12V meer over de condensator dan je zou denken, en bij ontladen juist 0,12V minder.
Bij het overgaan van laden naar ontladen zou je in dit voorbeeld dus een spanningssprong van 0,24V zien.
Maar die spanningsstap heeft niets met tijd te maken.

@Robin F.: al met al zou de maximale ontlaadstroom dus gelijk zijn aan de spanning op de C gedeeld door de ESR (+ alle andere weerstanden in de draden en zo).

Eigenlijk, als we het niet àl te ingewikkeld maken, is de ESR gewoon een (hopelijk kleine) weerstand in serie met de capaciteit, en de lekweerstand een (hopelijk grote) weerstand parallel aan de capaciteit.
Een elko met een idioot hoge ESR zou dus nog best een prima capaciteit en bijna geen lek kunnen hebben (even afgezien van de oorzaak van de hoge ESR, want sommige oorzaken kunnen misschien ook wel de capaciteit aantasten - daar ga ik niet over ).

Op 27 april 2010 00:03:51 schreef Omicron:
Ben je daar wel helemaal zeker van?

Bij een steilere flank is er meer vermogen aanwezig in de hogere harmonischen.

FET: dat is wat ik in eerste instantie wilde weten. Door de metingen ben ik er ook achter gekomen hoe je het kunt meten. Dat heb ik dus goed gedaan. Maar nu weet ik ook wat die spanningsval betekent.

Dan over dat graden verhaal. Ik weet niet meer waar ik het gevonden heb. Op de site van Freddy staat ook iets over graden maar daar was het niet. Ik heb te veel literatuur over netwerk analyse en een te slecht geheugen. Ik las het toen ik met smith chards bezig was. Dat verhaal over de kleinste meetfout (esr/reactantie) komt we wel vaag bekend voor. Iets in die strekking staat volgens mij ook in Bowick.

Maar capaciteit is Q/V daar is geen frequentie afhankelijk element. Misschien veranderd de Q(lading in coulomb) wel door de Vf van het gebruikte dielictrium en daarmee dus de capaciteit. Om met de bus van Free te spreken. De deur is te klein en er willen al mensen naar binnen voor de oude eruit zijn. Of veranderd permittivity van het dielectrium met de frequentie. Geen idee eigelijk maar als je een condensator meet veranderd met de frequentie de reactantie maar ook de capaciteit.

Agilent heeft een AN over het meten van dit soort dingen, helaas staat er niet bij hoe je de ESR, ESL en Xc splitst. Ze geven alleen het resultaat na een S21 meting. Overal staat bij hoe ze dat berekenen maar hier net niet. Die HP zal wel als feature hebben dat je dat zo uitleest. Mijn VNA heeft dat ook maar dan voor S11 metingen. Ik zal het nog eens goed na lezen. Het was al laat gisteren. Ze doen daar een soort kelvin meting. Dat blijkt met de vna prima te gaan door een S21 shunt meting. Dan heb je een dynamisch bereik van 90dB en ik kan direct R-xj aflezen. Alleen is xJ dan capaciteit en inductie maar R is natuurlijk puur R en dus de ESR (en bij mijn HP heb ik zelfs meer dan 110dB bereik maar dan moet ik zelf rekenen)

[Bericht gewijzigd door fred101 op dinsdag 27 april 2010 15:08:53 (15%)]

wat hebben snijbieten te maken met smith kaarten ? ( Chards zijn zilverbieten ,ook wel snijbieten genoemd)

Op 27 april 2010 14:33:48 schreef Xenobinol:
Bij een steilere flank is er meer vermogen aanwezig in de hogere harmonischen.

Nochtans gaf ik een voorbeeld waar het tegengestelde het geval is. Hogere harmonischen kunnen een flank even goed minder steil maken.

Zou het niet eerder zo zijn dat hoge frequentie componenten in het fourier spectrum ontstaan door "scherpe bochten" in het tijdsdomein en niet zozeer door "steile hellingen"? Maar dat is misschien voer voor een andere draad.

Ja, maar die steilheid wist die arme sinus maar op een klein stukje rond het midden te halen; de driehoek won over het hele stuk. .

Een steile helling, die wèl op tijd moet stoppen om de amplitude niet te groot te maken, vraagt inderdaad om hogere spectrale bestanddelen. Dat van die scherpe bochten ga je dan wel tegenkomen.
(Hoewel theoretisch een enkele stap natuurlijk ook al oneindig breed in spectrum is.)

Vandaar die ratelstoring die je van een gelijkrichter kunt hebben. Hoe groter de elko (toch nog on topic ), hoe hoger èn smaller de stroomimpulsen en hoe vervelender de harmonischen van 50 (100) Hz kunnen zijn die je in de laadstroom vindt.

http://www.emcesd.com/tt020100.htm

Hier staat nog een andere manier om ESR te meten. Je stuurt een puls door een 50 ohm weerstand in serie met de C en bekijkt met een Hi-Z probe het resultaat. Bij het stijgen van de puls ontstaat een spanningspiek tgv de ESL en die is met de beruchte di/dt te berekenen. Zonder ESL en een perfecte puls zou de spanning direct wat omhoogschieten. Dat is de spanningsval over de ESR. Daarna begint de elco langzaam te stijgen. Die knik, of net na de ESL spike meet je de spanningsval en berekent de ESL.

Ook een mooie methode vind ik. Zo ver ik begrijp moet je puls lengte gewoon behoorlijk lang zijn en er hoeft niet met stroombronnen gewerkt te worden en de Xc maakt dus ook niet uit. Zie ik dat goed ?

Die meting is in beginsel heel eenvoudig te begrijpen. Hij meet de drie dingen bijna helemaal apart.

X_C is meer een sinus-ding, en je werkt hier niet met een sinus; maar de C maakt wel uit: die bepaalt de helling van de oplaadcurve.

Eigenlijk gebruik je wèl een stroombron: je gaat ervan uit dat over het hele plaatje de spanning over de condensator nog klein is, zodat de stroom gelijk aan de open pulsspanning gedeeld door 100 ohm (50 van de generator en 50 in de plug) zou zijn.

De gebruikelijke (puls) ESR metertjes bepalen óók op deze manier de serieweerstand, maar met de ESL doen ze niets.

Ik heb nu blijkbaar de goede keywords gebruikt want ik heb nu een hele hoop gevonden over ESR meten. Dan niet een variant op het gebruikelijke pulsmetertje maar ook AN's van fabrikanten en die werken meestal met de methode als in mijn link of net omgekeerd. De C wordt met DC geladen en dan over een weerstand ontladen en daarbij speelt de ESL blijkbaar minder.

D-metingen zijn niet omzetbaar naar ESR en ESR is niet frequentie afhankelijk. Dit las ik in een AN van Sencore, die maken blijkbaar nog al prijzige ESR metertjes.
The confusion appears to come from the formulas which attempt to convert the "D" (dissipation factor) reading from an AC impedance bridge to an ESR value. ESR, however, is only one of the many capacitor imperfections that causes poor D readings.
D also includes the effects of leakage resistance, equivalent series inductance, dielectric absorption, dielectric stress, and losses (such as water molecule resonance)
in the dielectric. Most of these other losses are frequency selective, so any attempt to calculate ESR from D will make it seem that ESR varies with frequency.

Ik leer iedere dag op dit forum, maar ik moet zeggen:
het vaakst leer ik dat nieuwe woorden, en de kersverse bedenkers van die woorden, het er allemaal niet makkelijker op maken.

Vroeger had je helemaal geen ESR (als woord, dan)!
In die goede oude tijd had je gewoon je diëlektrische verliezen (frequentieafhankelijk) en de ohmse verliezen (bijna niet frequentieafhankelijk).
(Lek is ook ohms verlies, maar speelt eigenlijk alleen bij elko's.)

Een mica-draaicondensator had bijvoorbeeld een lagere Q (voor de HF jongens; anderen zouden dus zeggen: een slechtere D) door de verliezen in het mica.
Dat was niet moeilijk te begrijpen.

Bij ontkoppelcondensatoren moest je om de zelfinductie van de wikkels en de aansluitdraden denken. Sommige amateurs maakten er zelfs misbruik van, door een condensator te kiezen die op de gebruiksfrequentie expres resoneerde met zijn eigen serieinductie.

In pulscondensatoren, zoals in ouderwetse radar- en laserapparatuur, waar grote pulsstromen geleverd moesten worden, was de serieinductie ook wel interessant, maar was vooral de serieweerstand dan weer de beperkende factor.

Dat laatste is ESR gaan heten, de anderen zijn vergeten geraakt, toen zijn ze op verschillende manieren verliezen gaan meten, en toen waren ze verbaasd.

Zó ongeveer moet het gegaan zijn..

Heel vroeger dan Jou naamgenoot gebruikte in 1955 de term Equivalent Series Resistance maar korte het niet af. In 1943 had hij het alleen over the series resistance welke getekend was in een plaatje wat, in zijn woorden, het equivalent van een condensator voorstelde.

Maar er werd toen wel heel uitgebreid ingegaan op de powerfactor en alle mogelijke soorten verliezen in alle soorten condensators tot parallel draden toe. Dat is de sinus van de phase angle in radians. De hoek welke de phase afwijkt van 90 graden. De tangens daarvan is D en de omkeerwaarde Q. Blijkt het allemaal al heel uitgebreid in mijn "bijbel" te staan

Vanavond wat metingen gedaan. Ik heb nu gewoon een bnc parallel met de meetweerstand van het ESR metertje gezet. Ik heb er via een opamp ook een meter achter gezet. De meter keurig met weerstanden geijkt van 0 tot 10 ohm. Daarna de ESR van een partijtje +200uF elco's bij 130KHz gemeten. Daar klopte helemaal geen hout van. Ik denk dat die spikes roet in het eten gooien. Hij gaf bij 300 mOhm bv minder aan als bij 170 mOhm en 93 mOhm zat daar ergens tussen in. Maar dat is niet erg. Via de scope gaat het net zo snel en je hoeft eigenlijk niet eens te rekenen. Je ziet het vrij snel zo.

Morgen ga ik die andere manier proberen en dan wat elco's daarna met de vna nameten op de zelfde frequentie via S11 en S21. Dan zet ik alle metingen eens naast elkaar. Leuk weer wat spelen

Misschien kan ik beter zeggen: het populariseren van die woorden.
Net als bij veel andere theoriën (Gödel's theorema; Omega3 vetzuren, ...) wordt er dan één begripje uitgevist en opgeblazen, zonder naar de rest te kijken.
Dan heb je opeens een hype, maar door de onvolledigheid gaan er dan dingen mis in het begrip.

Ik vind het prachtig, die vergelijkende metingen die je doet. Daar hebben een hoop mensen plezier van, vooral doordat je ze ook op je website (log? dagboek?) publiceert.

Bij deze de resultaten van de nodige metingen en overdenkingen. De voorzichtige conclusie (van mij) is dat die zelf-bouwmeters niet werken .
Ik heb nog een tweede manier gevonden om met de vna dit te meten en dat wijkt wat af van de eerste meting maar dat kan bij wijze van spreken ook met een langer pootje of andere temperatuur te maken hebben.

De blokgolfmeters met diode detector kunnen volgens mij geen ESR meten want de ESR is geen constante waarde. Een topdetector wordt door de ESL en Xc beinvloedt en laat de ESR bij de alternatieve methode nu net de top niet zijn maar het dal in de meting Daarnaast heb ik gemerkt dat de dutycycle daarbij invloed heeft. Zet ik bij 50% de meter bv op 10 dan loopt deze bijna gelijk met de dutycycle mee terug. (Je kan hem wel mooi als duty-cycle-meter gebruiken.)

http://www.hamforum.nl/viewtopic.php?f=80&t=1335